Answer:
79 marks are required to get a B or higher.
Explanation:
We have been given that the marks on a statistics test are normally distributed with a mean of 62 and a variance of 225. The instructor wishes to assign Bs or higher to the top 25% of the students in the class.
We will use normal distribution table and z-score formula to solve our given problem.
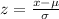 , where,
, where,
z= Z-score,
x = Sample score,
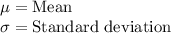
We know that standard deviation is equal to square-root of variance, so SD for given data would be
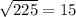 .
.
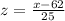
We know that top 25% means 75% and more.
Let us find z-score corresponding to 75% or 0.75 using normal distribution table.
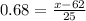
Let us solve for x.
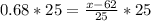
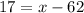
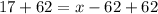
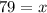
Therefore, 79 marks are required to get a B or higher.