Answer: 6.68%
Explanation:
Given : The mean weekly income of electrical engineers in NJ is $1,200 with a standard deviation of $200.
i.e.
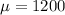 and
and
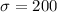
Let x denotes the monthly income ( in dollars).
If normally distributed , then the probability of workers earn more than $1,500 :
![P(x>1500)=1-P(\leq1500)\\\\=1-P((x-\mu)/(\sigma)\leq(1500-1200)/(200))\\\\=1-P(z\leq1.5)\ \ [\because\ z=(x-\mu)/(\sigma)]\\\\ =1-0.9332\ \ [\text{By z-table}]\\\\=0.0668=6.68\%](https://img.qammunity.org/2021/formulas/mathematics/college/ssio5y0dl2n7wfm6g33nli7pvawd1vn9jq.png)
Therefore , the percentages of workers earn more than $1,500 = 6.68%