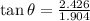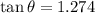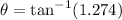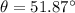Question

An m2 = 1.2 kg can of soup is thrown upward with a velocity of v2 = 6.8 m/s. It is immediately struck from the side by an m1 = 0.37 kg rock traveling at v1 = 8.6 m/s. The rock ricochets off at an angle of α = 61◦ with a velocity of v3 = 5 m/s. What is the angle of the can’s motion after the collision? Answer in units of ◦ .

Answer 1

Step-by-step explanation:

Given

mass of can
`m_2=1.2\ kg`

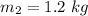
mass of rock
`m_1=0.37\ kg`

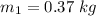
upward of can
`v_2=6.8\ m/s`

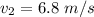
velocity of rock
`v_1=8.6\ m/s(Horizontal)`

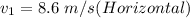
ricochets off angle
`\alpha =61^(\circ)`

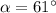
Velocity of rock after collision
`v_3=5\ m/s`

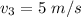
Let velocity of can after collision is
`v_4`

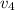
suppose can makes an angle of
`\theta` with horizontal

as External motion is absent therefore we can conserve momentum

Conserving momentum in x direction

`m_1v_1+0=m_1v_3\cos \alpha +m_2v_2\cos \theta`

`0.37* 8.6+0=0.37* 5* \cos (61)+1.2* v_4* \cos \theta`

`v_4\cos \theta =1.904 -------1`

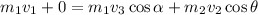
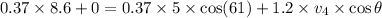
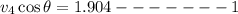
Conserving momentum in Y direction

`0+m_2v_2=m_1v_3\sin \alpha +m_ 2v_4\sin \theta`

`1.2* 6.8=1.2* 5* \sin (61)+1.2* v_4\sin \theta`

`v_4\sin \theta =2.426 --------2`

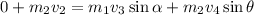
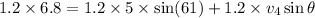
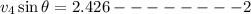
squaring and adding 1 and 2 we get

`v_4^2=9.511`

`v_4=3.084\ m/s`

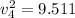
For angle
`\theta` divide 1 and 2

`\tan \theta =(2.426)/(1.904)`

`\tan \theta =1.274`

`\theta =\tan ^(-1)(1.274)`

`\theta =51.87^(\circ)`