Answer:
Part 1) The graph in the attached figure
Part 2) The value of s is approximately 45 km/sec
Explanation:
The complete question is
The function d=0.006s² represents the braking distances d in meters of a car at a speed s in kilometer per second.Graph the function. Then use your graph to estimate the speed of the car if its braking distance is 12 meters
Part 1) Graph the function
Let
s ----> the speed in kilometers per second
d ----> the braking distances in meters
we have
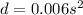
This is a quadratic equation (vertical parabola) open upward (the leading coefficient is positive)
The vertex represent a minimum
The vertex is the origin
The axis of symmetry is the y-axis
Find the values of d for different values of s
so
For s=0 km/sec ---->
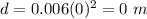 ---> point (0,0)
---> point (0,0)
For s=20 km/sec ---->
 ---> point (20,2.4)
---> point (20,2.4)
For s=30 km/sec ---->
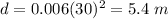 ---> point (30,5.4)
---> point (30,5.4)
For s=40 km/sec ---->
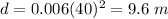 ---> point (40,9.6)
---> point (40,9.6)
For s=50 km/sec ---->
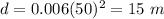 ---> point (50,15)
---> point (50,15)
To graph the function plot the points and connect them
see the attached figure
Part 2) Use your graph to estimate the speed of the car if its braking distance is 12 meters
Looking at the graph
For d=12 m
The value of s is approximately 45 km/sec
see the attached figure