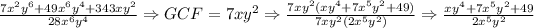Question

For each rational expression, identify the greatest common factor, write the expression in factored form, and simplify.

show all work leading to answer.

27a^4/3a^3

15m^5 n/ 25m^2n^6

x^4+x^6/ x^3

a^5/a^9-a^4

3b^2+b/5b^4

9x^2y^3+x^2y^2/2x^3y^4

21y^3/7y^4-14y^2

6x^4+12x^3-3x^2/9x^2

2p^5 q- 10pq^3/ 4p^3q^4+12p^5q^3



Write your own example of a rational expression and demonstrate how to simplify the expression using GCF (greatest common factor).

Write a rational expression with a gfc that has both a numeric part and a variable part.

Identify gfc and show how to simplify using gfc.

Write two sentences describing how you simplified expression using gfc.

Answer 1

1)
`9a,\frac{3^(3n)}{5^{n^(5)}},(x+x^(3))/(x^(3)),(a)/(a^(5)-1),(3b+1)/(5b^(3)), (3y)/(y^(2)-2),(2x^(2)+4x-1)/(3), ((p^(4)-5q^(2)))/((2p^(2)q^(3)+6p^(4)q^(2)))` 2)
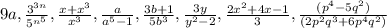`(xy^(4)+7x^(5)y^(2)+49)/(2x^(5)y^(2))`

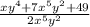
Prime factorize the parameters 7,49,28,343 pick its GCF=7. As for the variables choose the ones raised to the least exponent and divide each term by this.

Then, after that part. All that's left is a simplification dividing the members by the common monomial.

Explanation:

1) Let's proceed this way. For the numbers, to find the GCF is simply to Prime factor the numbers and pick greatest common factor. When it comes to variables the point is to choose the variable with the least exponent.

`(27a^(4))/(3a^(3))\: GCF=3a^(3)\Rightarrow (27a^(4):3a^3)/(3a^(3):3a^(3))=9a\\\\\frac{15m^(5n)}{25m^{2n^(6)}}\:GCF=5 \Rightarrow \frac{15m^(5n):5m^(2n)}{25m^{2n^(6)}:5m^(2n)}=\frac{3^(3n)}{5^{n^(5)}}\\\\(x^(4)+x^(6))/(x^(3))\:GCF=x^3\Rightarrow (x^(4):x^(3)+x^(6):x^(3))/(x^(3):x^(3))\Rightarrow (x+x^(3))/(x^(3))`

`(a^(5))/(a^(9)-a^(4))\:GCF:a^(4)\Rightarrow (a^(5):a^(4))/(a^(9):a^(4)-a^(4):a^(4))\Rightarrow (a)/(a^(5)-1)\:or\:(a^(4)(a))/(a^(4)(a^(5)-1))=(a)/(a^(5)-1)\\(3b^(2)+b)/(5b^(4))\:GCF=b\Rightarrow (b(3b+1))/(b(5b^(3)))=(3b+1)/(5b^(3))\\(21y^(3))/(7y^4-14y^2)\:GCF=7y^(2)\Rightarrow (7y^(2)(3y))/(7y^(2)(y^(2)-2))\Rightarrow (3y)/(y^(2)-2)`

`(6x^(4)+12x^(3)-3x^(2))/(9x^(2))\:GCF=3x^(2)\Rightarrow (3x^(2)(2x^(2)+4x-1))/(3x^(2)(3))\Rightarrow (2x^(2)+4x-1)/(3)`

`(2p^(5)q-10pq^(3))/(4p^(3)q^(4)+12p^(5)q^(3))\:GCF=2pq \Rightarrow (2pq(p^(4)-5q^(2)))/(2pq(2p^(2)q^(3)+6p^(4)q^(2)))=((p^(4)-5q^(2)))/((2p^(2)q^(3)+6p^(4)q^(2)))`

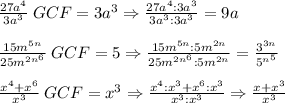
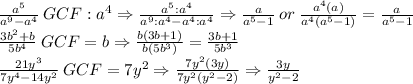
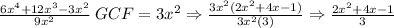
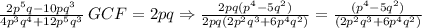
2,3) Write your own example of a rational expression and demonstrate how to simplify the expression using GCF (greatest common factor).

Write a rational expression with a gfc that has both a numeric part and a variable part.

Identify gfc and show how to simplify using gfc.

Well, similarly, to the previous ones. Prime factorize the parameters 7,49,28,343 pick its GCF=7. As for the variables choose the ones raised to the least exponent and divide each term by this.

Then, after that part. All that's left is a simplification dividing the members by the common term as it follows:

`(7x^(2)y^(6)+49x^(6)y^(4)+343xy^(2))/(28x^(6)y^(4))\Rightarrow GCF=7xy^(2)\Rightarrow (7xy^(2)(xy^(4)+7x^(5)y^(2)+49))/(7xy^(2)(2x^(5)y^(2)))\Rightarrow (xy^(4)+7x^(5)y^(2)+49)/(2x^(5)y^(2))`