Question

Suppose a marketing company wants to determine the current proportion of customers who click on ads on their smartphones. It was estimated that the current proportion of customers who click on ads on their smartphones is 0.62. How many customers should the company survey in order to be 92% confident that the margin of error is 0.27 for the confidence interval of true proportion of customers who click on ads on their smartphones?

Answer 1

Answer: 10 customers.

Explanation:

The formula to find the required sample size :

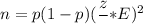`n=p(1-p)(\frac z^*}{E})^2` (1)

, where p= prior population proportion.

n= sample size.

`\sigma` = Population standard deviation from previous studies.

Let p be prior population proportion of the customers who click on ads on their smartphones .

As per given , we have

p=0.62

E= 0.27

For 92% confidence , significance level :
`\alpha=1-0.92=0.08`

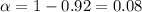
The critical value of z for 92% confidence interval from z-table would be

`z_(\alpha/2)=z_(0.04)=1.75`

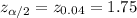
Put theses values in the formula (1), we will get

`n=(0.62)(1-0.62)(((1.75))/(0.27))^2`

`n=(0.2356)(6.48148)^2= 9.89745775254\approx 10`

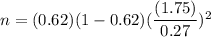
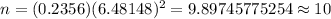
Therefore , the company should survey 10 customers .