Explanation:
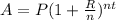
A = Amount after t time period
P = Principal amount
R = Interest rate
n = Number of times interest applied per time period
We have:
a) P = $1,500
R =5%=0.05
n = 1
t = 3 years
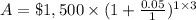

The amount after 3 years in the bank will be $1,736.43.
b) P = $1,500
R =5%=0.05
n = 1
t = 18 years
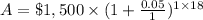
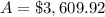
The amount after 3 years in the bank will be $3,609.92.
c) P = $1,500
R =5%=0.05
n = 1
t = ?
A= $2,000
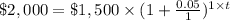
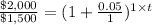
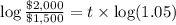

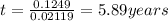
5.89 years will it take for the account to contain $2,000.
d) P = $1,500
R =5%=0.05
n = 1
t = ?
A= $2,500

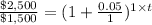
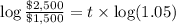

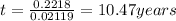
10.47 years will it take for the account to contain $2,000.