Question

If the probability of rain on any given day in Chicago during the summer is 50%, independent of what happens on any other day, what is the probability of having exactly 3 rainy days from July 4 through July 8, inclusive?

Answer 1

Answer: 0.3125

Explanation:

Given : The probability of rain on any given day in Chicago (independent of what happens on any other day) during the summer is 50% =0.5

Number of days from July 4 through July 8, inclusive = 5

According to the Binomial distribution for any random variable X , the probability of getting x successes in n trials :

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

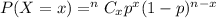
, where p is the probability of getting success in each trial.

Let x = number of rainy days .

As per given , we have n= 5 , p=0.5

Then, the probability of having exactly 3 rainy days from July 4 through July 8, inclusive will be
`P(X=3)=^5C_3(0.5)^3(1-0.5)^(5-3)`

`=(5!)/(3!(5-3)!)(0.5)^5\\\\=(5*4*3!)/(3!(2)!)(0.03125)=10(0.03125)=0.3125`

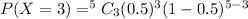
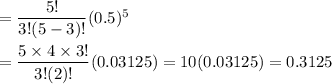
Hence, the probability of having exactly 3 rainy days from July 4 through July 8, inclusive= 0.3125