Question

A couple has two children, what is the probability that both children are girls given the fact the older child is a girl?

Answer 1

`(1)/(2)`

Explanation:

Let g represent the girl child of the parent, and

Let b represent the boy child of the parent.

The sample space S of the possibilities of two children is

S = (g,g), (g,b), (b,g), (b,b)

The first element of the each of the event in the sample space is the eldest child.

We have to consider some events, to get the probability that both children are girls given the fact the older child is a girl.

Event A, the two children are girls. We have one outcome (g,g)

so A = (g,g)

Event B, the eldest child is a girl. We have two outcomes (g,b) and (g,g)

so B = (g,b), (g,g)

Therefore,

`P(A|B) = (P(AnB))/(P(B))`

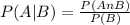
Solving the numerator,

`P(AnB) = (|A n B|)/(|S|)`

`P(AnB) = (1)/(4)`

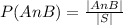
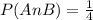
Solving the denominator,

`P(B) = (|B|)/(|S|)`

`P(B) = (1)/(2)`

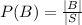
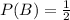
Then,

`P(A|B) = (1/4)/(1/2)`

`P(A|B) = (1)/(2)`

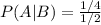
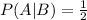
The probability that both children are girls given the fact the older child is a girl is
`(1)/(2)`