Answer:
y−coordinate is 2.
Explanation:
It is given that P(−1,4),Q(1,−2), with K a point on the perpendicular bisector of PQ.
K is in the first quadrant at a distance of √10 units from PQ.
Let the coordinates of K are (a,b) where a and b are non negative.
A be the midpoint of PQ is
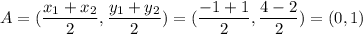
Slope of PQ is
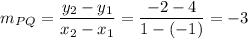
PQ and AK are perpendicular. It means Product of their slopes is -1.
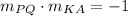
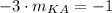
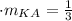
Point slope form of a line is
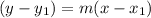
where, m is slope.
Equation PQ is
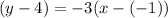
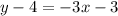
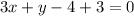
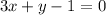
Similarly. equation of AK is
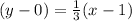
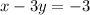
It passes through (a,b) so
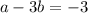 ... (1)
... (1)
The distance of a point
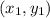 from the line
from the line
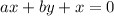 is
is
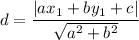
It is given that the distance between K and PQ is √10.
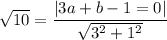
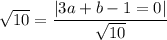
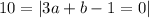
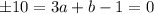
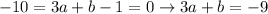 .... (2)
.... (2)
 ... (3)
... (3)
On solving (1) and (2) we get
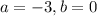
On solving (1) and (3) we get
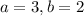
We know that K is in the first quadrant. It means a≥0 and b≥0.
Therefore, y−coordinate is 2.