Question

A sociology professor asks her class to observe cars having a man and a woman in the front seat and record which of the two is the driver.a. Explain why it is reasonable to use the binomial distribution for the number of the male drivers who own cars if all observations are made in the same location at the same time of day.b. Explain why the binomial model may not apply if half the observations are made outside a church on sunday morning and half are made on campus after a dance.c. The professor requires students to observe 10 cars during business hours in a retail district close to campus. Past observations have shown that the man is driving about 85% of cars in this location. What is the probability that the man is driving 8 or fewer of the 10 cars?d. The class has 10 students who will observe 100 cars in all. What is the probability that the man is driving 80 or fewer of these?

Answer 1

Answer to Question (a)

It is reasonable to use binomial distribution because it can be assumed that the no one being observed is aware of the process, hence the observation can be considered to be independent. Furthermore the probability of “success” i.e. getting the desired result can be assumed to be constant since it cannot be influenced by different condition because both a man and a woman are required to be in the car

Answer to Question (b)

Binomial model may not apply because the condition are not the same and for reason which are sociological, the probability that a man drives may be different in these two circumstances.

Answer to Question (c) is = 0.4557001764

Answer to Question (d) is = 10.38% or 0.1038

Step-by-step explanation:

In order to gain a better understanding of the the answers above we to understand few terms

Binomial Distribution :

The binomial distribution is a discrete probability distribution used when there are only two possible outcomes for a random variable: success and failure. Success and failure are mutually exclusive; they cannot occur at the same time.

Normal Approximation :

A normal approximation can be defined as a process where the shape of the binomial distribution is estimated by using the normal curve

The step-by-step answer to question c

The total number of men X driving, among the 12 observations made is B (12, 0.85), the general formula for binomial distribution is given below

(First uploaded image)

Where X is the random variable, n is the number of trials, k is the number of successes and p is the probability of success. Substituting the value we get the equation shown below

(Second uploaded image)

From the equation on the third image we see that the () was introduced, because are looking for the probability that the men are equal to 8 or fewer and causes a little change to the general equation by introducing the summation of result.

From the equation on the second image we have

(Third uploaded image)

The step-by-step answer to question d

Step 1: Find p,q, and n:

The probability p (i.e the probability of success) is given in the question as 85%, or 0.85

To find q(the probability of failure), subtract p from 1: 1 – 0.85 = 0.15

The sample size n is given in the question as 100

Step 2: Figure out if you can use the normal approximation to the binomial. If n * p and n * q are greater than 5, then you can use the approximation:

n * p = 85 and n * q = 15.

These are both larger than 5, so you can use the normal approximation to the binomial for this question.

Step 3: Find the mean, μ by multiplying n and p:

n * p = 85

(You actually figured that out in Step 2!).

Step 4: Multiply step 3 by q :

`85 * 0.15 = 12.75.`

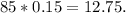
Step 5: Take the square root of step 4 to get the standard deviation, σ:

`√(12.75)=  3.57`

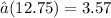
Note: The formula for the standard deviation for a binomial is √(n*p*q).

Using the Continuity Correction Factor

First lets understand what Continuity Correction Factor is :

A continuity correction factor is used when you use a continuous probability distribution to approximate a discrete probability distribution. For example, when you want to use the normal to approximate a binomial.

There are some rules we need to understand:

if P(X = n)

Step 6: Write the problem using correct notation. The question stated that we need to “the probability that the man is driving 80 or fewer of these?”. So:

P(X ≤ 80)

Step 7: Rewrite the problem using the continuity correction factor:

`P(X ≤ 80)= P (X < 80+ 0.5) = P(X < 80.5)`

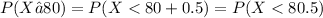
Step 8: Draw a diagram with the mean in the center. Shade the area that corresponds to the probability you are looking for. We’re looking for X ≤ 80.5, so:

Step 9: Find the z-score.

You can find this by subtracting the mean (μ) from the probability you found in step 7, then dividing by the standard deviation (σ):

z =
`(80.5 – 85) / 3.57 = -1.26`

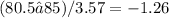
This mean that we are moving from the X dimension to the Z dimension

P(Z < z)

P(Z < -1.26)

Step 10: After calculating the standardized score, we need to look up the area (same as probability) using the z-table. First, we find the first two digits on the left side of the z-table. In this case it is -1.2. Then, we look up a remaining number across the table (on the top) which is 0.06 in our example. The corresponding area is 0.1038 which translates into 10.38%

That’s it! The probability is 0.1038, or 10.38%.