Question

If the sample contained 2.0 moles of KClO3 at a temperature of 214.0 °C, determine the mass of the oxygen gas produced in grams and the pressure exerted by the gas against the container walls.

Answer 1

Answer : The mass of the oxygen gas produced in grams and the pressure exerted by the gas against the container walls is, 96 grams and 1.78 atm respectively.

Explanation : Given,

Moles of
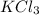`KCl_3` = 2.0 moles

Molar mass of
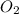`O_2` = 32 g/mole

Now we have to calculate the moles of
`MgO`

The balanced chemical reaction is,

`2KClO_3\rightarrow 2KCl+3O_2`

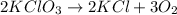
From the balanced reaction we conclude that

As, 2 mole of
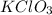`KClO_3` react to give 3 mole of
`O_2`

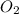
So, 2.0 moles of
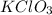`KClO_3` react to give
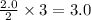`(2.0)/(2)* 3=3.0` moles of
`O_2`

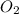
Now we have to calculate the mass of
`O_2`

`\text{ Mass of }O_2=\text{ Moles of }O_2* \text{ Molar mass of }O_2`

`\text{ Mass of }O_2=(3.0moles)* (32g/mole)=96g`

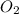
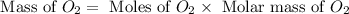
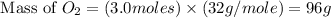
Therefore, the mass of oxygen gas produced is, 96 grams.

Now we have to determine the pressure exerted by the gas against the container walls.

Using ideal gas equation:

`PV=nRT\\\\PV=(w)/(M)RT\\\\P=(w)/(V)* (RT)/(M)\\\\P=\rho* (RT)/(M)`

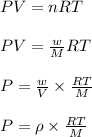
where,

P = pressure of oxygen gas = ?

V = volume of oxygen gas

T = temperature of oxygen gas =
`214.0^oC=273+214.0=487K`

R = gas constant = 0.0821 L.atm/mole.K

w = mass of oxygen gas

`\rho` = density of oxygen gas = 1.429 g/L

M = molar mass of oxygen gas = 32 g/mole

Now put all the given values in the ideal gas equation, we get:

`P=1.429g/L* ((0.0821L.atm/mole.K)* (487K))/(32g/mol)`

`P=1.78atm`

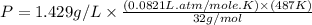
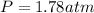
Thus, the pressure exerted by the gas against the container walls is, 1.78 atm.