Question

Find the zeros of the function y=x^2-4x-16 by completing the square. Express your answer in simple redical form. Graph the parabola using a standar window to see the irrational zeroes.

Answer 1

The zeros of the function are

`x=2+2√(5)`

`x=2-2√(5)`

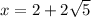
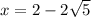
The graph in the attached figure

Explanation:

we have

`y=x^(2)-4x-16`

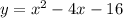
This is a vertical parabola open upward (the leading coefficient is positive)

The vertex is a minimum

Remember that

The zeros of the function are the values of x when the value of y is equal to zero

For y=0

`x^(2)-4x-16=0`

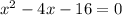
Move the constant term to the right side

`x^(2)-4x=16`

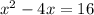
Complete the square

`x^(2)-4x+2^2=16+2^2`

`x^(2)-4x+4=20`

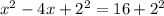
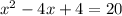
Rewrite as perfect squares

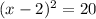`(x-2)^(2)=20` ---> the vertex is the point (2,-20)

take square root both sides

`x-2=\pm√(20)`

`x=2\pm√(20)`

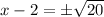
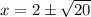
Simplify

`x=2\pm2√(5)`

The zeros of the function are

`x=2+2√(5)`

`x=2-2√(5)`

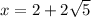
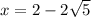
using a graphing tool

The graph in the attached figure