Question

In a​ lottery, 6 numbers are randomly sampled without replacement from the integers 1 to 50. Their order of selection is not important. Find the probability of holding a ticket that has zero winning numbers out of the 6 numbers selected for the winning ticket out of the 50 possible numbers.

Answer 1

Answer: 0.444225

Explanation:

Given : The total number of tickets = 50

Number of tickets are randomly sampled without replacement =6

Since the order of selection is not important , so we use combinations.

Total number of ways to select 6 tickets =
`^(50)C_6`

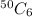
The number of winning tickets = 6

So, number of tickets that are not winning = 50-6=44

Number of ways of selecting zero winning numbers=
`^(44)C_(6)`

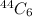
Now , the probability of holding a ticket that has zero winning numbers out of the 6 numbers selected for the winning ticket out of the 50 possible numbers would be
`(^(44)C_(6))/(^(50)C_6)`

`=((44!)/(6!(44-6)!))/((50!)/(6!(50-6)!))\\\\\\=((44*43*42*41*40*39*38!)/(38!))/((50*49*48*47*46*45*44!)/(44!))\\\\\\=(44*43*42*41*40*39)/(50*49*48*47*46*45)\\\\=(252109)/(567525)\approx0.444225`

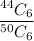
Hence, the required probability = 0.444225