Answer:
The expected number of siblings is 1.05 or 1 (when rounded)
Explanation:
Given the probability distribution of siblings of students in a high school with 1500 students:
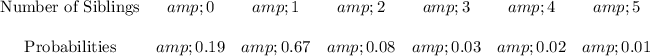
To find the expected value for the number of siblings of a randomly chosen student, myltiply the number of siblings by its probability and add all these products:

Thus, the expected number of siblings is 1.05 or 1 (when rounded)