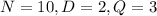Answer:
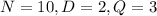
Explanation:
Notation
N= represent the number of nickels
D= represent the number of dimes
Q= represent the number of quarters
Solution to the problem
For this case we assume that a nickels represent 5 cents, a dime 10 cents and a quarter 25 cents. We know that the total ofor the 15 coins it's 1.45 or 145 cents. So we can set up the following equations:
 (1)
(1)
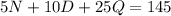 (2)
(2)
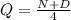 (3)
(3)
The condition (3) is obtained from the statement "the number of quarters is 1/4 the number of nickels and dimes combined"
So on this case we have a linear system of 3 equation with 3 values unknown so then this system can be solved.
We can use substitution in order to solve the values.
We can rewrite the quation (3) on this way
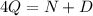
And if we replace this into equation (1) we got:
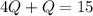
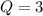
And know we can use the following two equations:
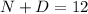 (1)
(1)
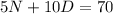 (2)
(2)
If we solve N from equation (1) we got:
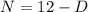 and if we replace this into equation (2) we got:
and if we replace this into equation (2) we got:

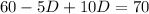
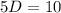
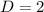
And then we can solve for N like this:
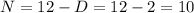
So then our final solution would be: