Question

Joel wants to fence off a triangular portion of his yard for his chickens. The three pieces of fencing he haas to use are 8 feet, 15 feet, and 20 feet long. Will he be able to make a right triangle with his fencing? Why or why not?

Answer 1

9514 1404 393

Answer:

no (maybe)

Explanation:

The Pythagorean theorem can be used to find the necessary length for the longest side:

8² +15² = s²

64 +225 = 289 = s²

s = √289 = 17

The fence pieces used as is will form an obtuse triangle. The longest piece of fence is longer than the length necessary for a right triangle.

If the pieces are used as is, a right triangle cannot be formed.

__

If the longest piece is cut to a length of 17 feet, then a right triangle can be formed.

Answer 2

No, it will not be able to make a right triangle.

Solution:

Given that,

Joel wants to fence off a triangular portion of his yard for his chickens.

The length of three peices of fencing are 8 feet , 15 feet and 20 feet

For making it a right triangle it must satisfy the "Pythagorus theorem"

Pythagorean theorem, states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle.

For a right angled triangle with sides a, b, c

`c^2 = a^2+b^2`

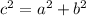
Given sides are:

a = 8 feet

b = 15 feet

c = 20 feet

Substituting the values in above formula

`20^2 = 8 ^2+15^2\\\\400 = 64 + 225\\\\400\\eq 289`

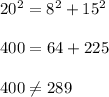
Since the pythogoras formula is not satisfied, the given sides cannot form a right angled triangle

Thus , No, it will not be able to make a right triangle.