Answer:
(a)
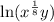
(b)
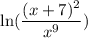
Explanation:
The given expression is
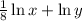
Using the properties of logarithm we get
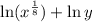
![[\because \ln a^b=b\ln a]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xtmf9gfxaggaxcrh3nkgqyh1hoqqfmdu7n.png)
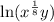
![[\because \ln(ab)=\ln a+\ln b]](https://img.qammunity.org/2021/formulas/mathematics/high-school/p7508pevj8prwjzd6ezbaf0y7f825p00w5.png)
Therefore, the simplified form of given expression is
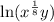 .
.
The given expression is
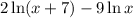
Using the properties of logarithm we get
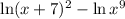
![[\because \ln a^b=b\ln a]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xtmf9gfxaggaxcrh3nkgqyh1hoqqfmdu7n.png)
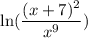
![[\because \ln((a)/(b))=\ln a-\ln b]](https://img.qammunity.org/2021/formulas/mathematics/high-school/toksyijkpkk9791l54sfp4niyv2isxaag5.png)
Therefore, the simplified form of given expression is
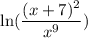 .
.