Question

A 2.00-kg, frictionless block is attached to an ideal spring with force constant 300 N/mN/m. At t=0 t=0 the block has velocity -4.00 m/sm/s and displacement +0.200 mm.

Find the amplitude.

Answer 1

The amplitude of the spring is 32.6 cm.

Step-by-step explanation:

It is given that,

Mass of the block, m = 2 kg

Force constant of the spring, k = 300 N/m

At t = 0, the velocity of the block, v = -4 m/s

Displacement of the block, x = 0.2 mm = 0.0002 m

We need to find the amplitude of the spring. We know that the velocity in terms of amplitude and the angular velocity is given by :

`v=\omega√(A^2-x^2)`

`\omega=\sqrt{(k)/(m)}`

`\omega=\sqrt{(300)/(2)}`

`\omega=12.24\ rad/s`

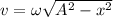
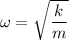
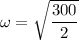
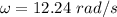
So,
`(v^2)/(\omega^2)+x^2=A^2`

`((-4)^2)/((12.24)^2)+(0.0002)^2=A^2`

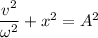
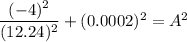
A = 0.326 m

or

A = 32.6 cm

So, the amplitude of the spring is 32.6 cm. Hence, this is the required solution.