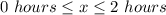Answer:
The linear function is

The reasonable domain is
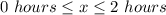
Explanation:
Let
x ----> the time in hours
y ---> the distance in miles
we know that
The linear equation in slope intercept form is equal to

where
m is the slope or unit rate
b is the y-intercept or initial value
In this problem
The slope is
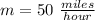
The y-intercept is

substitute

Find the domain for x
For y=120 miles
Find the value of x
substitute the value of y in the linear equation and solve for x
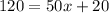

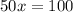
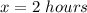
therefore
The domain is the interval [0,2]