Question

The formula h = -16t squared + 64t squared gives the height, h, and time, t, of an object launched from the ground with a speed of 64 feet per second. Find the heights at t = 0, 1, 2, 3, and 4 seconds. Explain what happened each second.

Answer 1

Details in the explanation

Step-by-step explanation:

Vertical Launch

When an object is thrown vertically in free air (no friction), it moves upwards at its maximum speed while the acceleration of gravity starts to brake it. At a given time and height, the object stops in mid-air and starts to fall back to the launching point until reaching it with the same speed it was launched.

We are given an expression for the height of an object in function of time t

`h = -16t^2 + 64t`

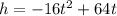
Please note we have deleted the second 'squared' from the formula since it's incorrect and won't describe the motion of vertical launch.

We now have to evaluate h for the following times, assuming h comes in feet

At t=1 sec

`h = -16(1)^2 + 64(1)=64-16=48\ ft`

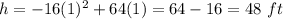
The object is at a height of 48 feet

At t=2 sec

`h = -16(2)^2 + 64(2)=128-64=64\ ft`

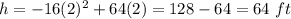
The object is at a height of 64 feet. This is the maximum height the object will reach, as we'll see below

At t=3 sec

`h = -16(3)^2 + 64(3)=192-144=48\ ft`

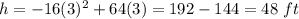
The object is at a height of 48 feet. We can clearly see it's returning from the maximum height and is going down

At t=4 sec

`h = -16(4)^2 + 64(4)=256-256=0\ ft`

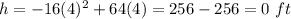
The object is at ground level and has returned to the launch point.