Question

Rounded to the nearest tenth, what is the area of rectangle ABCD? rectangle ABCD with diagonal AC, labeled as measuring 9 feet, angle BAC measuring 30 degrees, angle BCA measuring 60 degrees, angle DCA measuring 30 degrees, and angle DAC measuring 60 degrees A. 70.1 square feet B. 40.5 square feet C. 35.1 square feet D. 25.5 square feet E. 24.6 square feet

Answer 1

35.1 sq. feet.

Explanation:

Here ABCD is a rectangle and AC is a diagonal. Hence, Δ ABC is a right triangle with AC = 9 feet and ∠ CAB = 30°.

So, from the right triangle Δ ABC,

`\sin 30^(\circ) = (BC)/(AC) = (BC)/(9)`

⇒ BC = 9 sin 30° = 4.5 feet.

Again,
`\cos 30^(\circ) = (AB)/(AC) = (AB)/(9)`

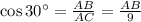
⇒ AB = 9 cos 30° = 7.794 feet.

Therefore, area of the rectangle is (AB × BC) = 4.5 × 7.794 = 35.1 sq. feet (Answer)