Question

Show timer Statistics

If a square region with side x and a circular region with radius r have the same area, then x must be how many times as great as r?
A. 1π1π
B. 1π√1π
C. π√π
D. ππ
E. π2

Answer 1

C.
`√(\pi)`

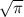
Explanation:

We have been given that a square region with side x and a circular region with radius r have the same area. We are asked to find that x must be how many times as great as r.

We know that area of a square is square of its each side length, so area of square region with side x would be
`x^2`.

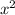We also know that area of circle is
`\pi r^2`.

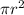Since we have been given that both areas are same, so we will equate both areas as:

`x^2=\pi r^2`

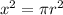
Let us take positive square root of both sides as:

`√(x^2)=√(\pi r^2)`

`x=√(\pi)\cdot √(r^2)`

`x=√(\pi)\cdot r`

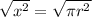
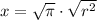
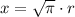
Let us divide both sides by r:

`(x)/(r)=(√(\pi)\cdot r)/(r)`

`(x)/(r)=√(\pi)`

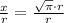
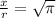
Therefore, x must be
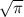`√(\pi)` times greater than r and option C is the correct choice.