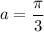Question

Two particles execute shm of same amplitude of 20 cm with same period along the same line about the same equilibrium position. the maximum distance between the two is 20 cm. their phase difference in radians is

Answer 1

`a=(\pi)/(3)`

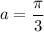
Step-by-step explanation:

given,

Amplitude ,A= 20 cm

distance between distance between two particle,y = 20 cm

Let equation of two SHM be x = A sin (ωt) and x = A sin (ωt + a)

where A is amplitude , ω is angular frequency and a is the phase difference.

now,

Distance between two particle at time t

y = A(sin(ωt+a)- sin (ωt))

using identity

`sin A - sin B = 2sin((A-B)/(2))cos((A+B)/(2))`

`y = A(2sin((a)/(2))cos((2\omega t + a )/(2)))`

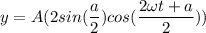
for maxima
`cos((2\omega t+a)/(2)) = 1`

maximum distance

`y = A(2sin((a)/(2)))`

`20 = 20 * 2 sin((a)/(2))`

`sin((a)/(2))=(1)/(2)`

`sin((a)/(2))=sin((\pi)/(6))`

`(a)/(2)=(\pi)/(6)`

`a=(\pi)/(3)`

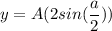
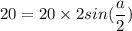
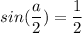
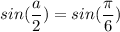
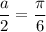
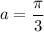
hence, the phase difference between the two particle is equal to
`a=(\pi)/(3)`