Question

You select a random sample of n=14 families in your neighborhood and find the following family sizes (number of people in the family)

15, 16, 19, 18, 17, 15, 16, 16, 15, 16, 15, 16. 17, 18

a. What is the best estimate for the mean family size for the population of all families in a country?

(round to the nearest tenth as needed)

b. What is the 95% confidence interval for the estimate?

__
(round to the nearest tenth as needed)

c. Comment on the reliability of the estimate. Choose the correct answer below.

The sample is unlikely to be very representative of all families in a country.

The sample is unlikely to be representative of all families in a country.

There is not enough data to make a conclusion.

Answer 1

a)
`\bar X = (\sum_(i=1)^n X_i )/(n)`

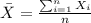
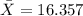`\bar X=16.357` represent the sample mean

b) The 95% confidence interval would be given by (15.620;17.094)

c) The concept of very representative not exists. A asmaple can be representative or not of a population. So then based on this the best option is:

The sample is unlikely to be representative of all families in a country.

The reason is because we have just a sample of 14 if we want to be more confidence about the true population mean we can increase the sample size in order to have a better estimation.

Explanation:

Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The data given : 15, 16, 19, 18, 17, 15, 16, 16, 15, 16, 15, 16. 17, 18

We can calculate the mean and the sample deviation with the following formulas:

`\bar X = (\sum_(i=1)^n X_i )/(n)`

`s= \sqrt{(\sum_(i=1)^n (x_i -\bar X)^2)/(n-1)}`

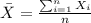
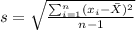
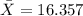`\bar X=16.357` represent the sample mean

`\mu` population mean (variable of interest)

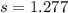`s=1.277` represent the sample standard deviation

n=14 represent the sample size

Part a

The best estimate for the mean is the average given by:

`\bar X = (\sum_(i=1)^n X_i )/(n)`

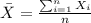
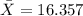`\bar X=16.357` represent the sample mean

Part b

The confidence interval for the mean is given by the following formula:

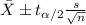`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The degrees of freedom are given by:

`df = n-1= 14-1 = 13`

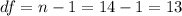
Since the Confidence is 0.95 or 95%, the value of
`\alpha=0.05` and
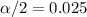`\alpha/2 =0.025`, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.025,13)".And we see that
`t_(\alpha/2)=\pm 2.16`

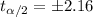
Now we have everything in order to replace into formula (1):

`16.357-2.16(1.277)/(√(14))=15.620`

`16.357+2.16(1.277)/(√(14))=17.094`

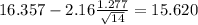
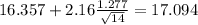
So on this case the 95% confidence interval would be given by (15.620;17.094)

Part c

The concept of very representative not exists. A asmaple can be representative or not of a population. So then based on this the best option is:

The sample is unlikely to be representative of all families in a country.

The reason is because we have just a sample of 14 if we want to be more confidence about the true population mean we can increase the sample size in order to have a better estimation.

Answer 2

a. Best estimate for the mean family size for the population of all families in a country is 16.3571428571

b. 95% confidence interval for the estimate is 16.3571428571±0.7106240840. That is between 15.6465187731 and 17.0677669411

c. The sample is unlikely to be very representative of all families in a country.

Explanation:

a. mean family size for the population of all families in a country can be estimated as sample mean, and calculated as:

`(15+ 16+ 19+ 18+ 17+ 15+ 16+ 16+  15+ 16+  15+ 16+ 17+ 18 )/(14)` ≈ 16.3571428571

b. 95% confidence interval for the estimate can be calculated using the equation CI=M±
`(t*s)/(√(N) )` where

• M is the mean estimate (16.3571428571)

• t is the corresponding statistic in the 95% confidence level and with 14 degrees of freedom (2.160)

• s is the standard deviation of the sample (1.2309777100)

• N is the sample size (14)

s can be calculated as square root of mean squared differences from the sample mean.

Thus 95% CI=16.3571428571±
`(2.160*1.2309777100)/(√(14) )` ≈ 16.3571428571±0.7106240840

The sample is unlikely to be very representative of all families in a country because as the sample data increases, estimate will improve.