Question

In 1992, the moose population in a park was measured to be 3570. By 1999, the population was measured again to be 3640. If the population continues to change linearly:

Find a formula for the moose population,
,P, in terms of ,t, the years since 1990.

Answer 1

The formula for the moose population is

`P=10t+3550`

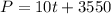
Explanation:

In 1992—that is, 2 years after 1990 or at
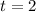`t=2`—the population
`P` is 3570, and in 1999 (
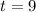`t=9`) population is 3640; so we have

`t=2,P=3570\\t=9,P=3640`

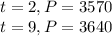
Now the formula that will model the moose population will be of the form:

`P=mt+b`

The slope
`m` is

`m=(3640-3570)/(9-2) =10`

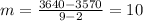
therefore we have

`P=10t+b`

Now we know that at
`t=2,`
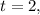
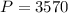`P=3570`, so we put these values in and solve for
`b:`

`3570=10(2)+b`

`b=3550`

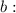
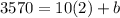
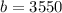
With this value of
`b`, we finally have the formula for the moose population:

`\boxed{P=10t+3550}`