Question

The legs of a right triangle are in the ratio of 3 to 1. If the length of the hypotenuse of the triangle is 40√40, then the perimeter of the triangle is between

A. 14 and 15
B. 13 and 14
C. 12 and 13
D. 11 and 12
E. 10 and 11

Answer 1

`P = 6+2+ √(40)=14.32`

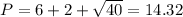
So then the best option on this case is:

A. 14 and 15

Explanation:

When we have a right triangle we can use the Pythegorean identity given by:

`Hip^2 = Opp^2 +Adj^2` (1)

Where Hip represent the hypothenuse. Opp represent the opposite side and Adj the adjacent side.

On this case we have given the hypothenuse assumed
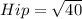`Hip = √(40)` because is the only possible reasonable value because
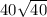`40√(40)` is a too much higher value

We have a ratio provided on this case, let's assume that the ratio is:

`(Opp)/(Adj) = 3`

`Opp = 3 Adj`

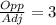
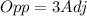
If we rpelace this condition into equation (1) we got:

`(√(40))^2 = (3Adj)^2 + Adj^2`

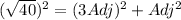
And then we have this:

`40 = 9 Adj^2 + Adj^2 = 10 Adj^2`

`Adj = \sqrt{(40)/(10)}=2`

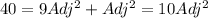
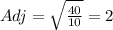
And then the opposite side is:

`Opp = 3 Adj =3* 2= 6`

The perimeter is defined as the sum of all the sides, we can find the perimeter like this:

`P = Opp + Adj + Hip`

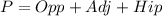
And replacing the values that we found we got:

`P = 6+2+ √(40)=14.32`

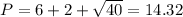
So then the best option on this case is:

A. 14 and 15