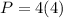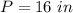Answer:
Part 1)
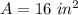
Part 2)
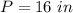
Explanation:
we know that
A cube has six equal square faces
A cross-section perpendicular to one face of the cube is equal to a square
see the attached figure to better understand the problem
Part 1) Find the area of the cross section
The area of the square is
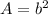
where
b is the length side of the square
we have
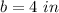
substitute

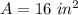
Part 2) Find the perimeter of the cross section
The perimeter of the square is
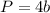
where
b is the length side of the square
we have
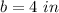
substitute