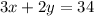Question

WORTH 50!! Answer it with explanation and the answer is not y+6 I have some idea on how to do this.

Answer 1

Therefore, equation of the line that passes through (16,-7) and is perpendicular to the line
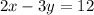`2x-3y=12` is
`3x+2y=34`

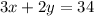
Explanation:

Given:

`2x-3y=12`

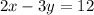
To Find:

Equation of line passing through ( 16, -7) and is perpendicular to the line

`2x-3y=12`

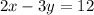
Solution:

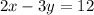`2x-3y=12` ...........Given

`\therefore y=(2)/(3)* x-4`

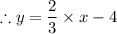
Comparing with,

`y=mx`

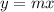
Where m =slope

We get

`Slope = m1 = (2)/(3)`

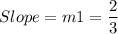
We know that for Perpendicular lines have product slopes = -1.

`m1* m2=-1`

Substituting m1 we get m2 as

`m2=-(3)/(2)`

Therefore the slope of the required line passing through (16 , -7) will have the slope,

`m2=-(3)/(2)`

Now the equation of line in slope point form given by

`(y-y_(1))=m(x-x_(1))`

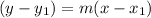
Substituting the point (16 , -7) and slope m2 we will get the required equation of the line,

`(y-7)=-(3)/(2)* (x-16)\\\\2y+14=-3x+48\\3x+2y=34......Equation\ of\ line`

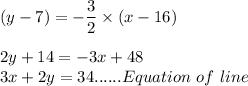
Therefore, equation of the line that passes through (16,-7) and is perpendicular to the line
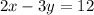`2x-3y=12` is
`3x+2y=34`