Question

A transmission is designed to last 16 years, with a standard deviation of 1.2 years. What is the probability that a transmission will last less than 14 years?

5%
20%
30%
35%

Answer 1

Answer A, 5%

Explanation:

Answer 2

First option 5%

Explanation:

Normal Distribution

Gauss Distribution is one of the most widely-used continuous probability distribution to characterize random events. The curve of the function is called the bell curve.

The standard Normal Distribution is a special case where the mean
`\mu=0` and the standard deviation
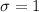`\sigma=1`. The values of the cumulative normal distribution cannot be computed by simple calculations, we must use tables of digital implementations integrated with tools like Excel or any online resource.

The entry for standard normal distribution is a parameter called the z-score, computed like shown below

`\displaystyle z=(X-\mu)/(\sigma)`

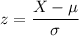
The values provided in our problem are

`X=14,\ \mu=16,\ \sigma=1.2`

Computing z results

`\displaystyle z=(14-16)/(1.2)=-1.667`

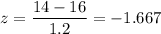
By using any of the aforementioned resources, we compute the left-tail probability

`P(z=-1.667)=0.048\approx 5\%`

We choose the first option 5%