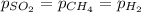Question

A mixture of 0.5 mol of CH4, 0.5 mol of H2, and 0.5 mol of SO2 is introduced into a 10.0 L container at 25 *C.

If the container has a pinhole leak, which describes the relationship between the partial pressures of the individual components in the containtainer after 3 hours?

(A.) PSO2 > PCH4>PH2.

(B.) PSO2
(C) PSO2 < PCH4 > PH2.

(D) PSO2= PCH4 = PH2.

Answer 1

Answer: The partial pressure of individual components in the container will be same, that is
`p_(SO_2)=p_(CH_4)=p_(H_2)`

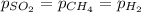
Step-by-step explanation:

To calculate the total pressure, we use the equation given by ideal gas equation:

`PV=nRT`

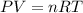
where,

P = pressure of the gas

V = Volume of gas = 10.0 L

n = Number of moles =
`(n_(CH_4)+n_(H_2)+n_(SO_2))=(0.5+0.5+0.5)=1.5mol`

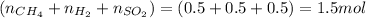
R = Gas constant =
`0.0821\text{ L atm }mol^(-1)K^(-1)`

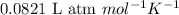
T = temperature of the gas =
`25^oC=[25+273]K=298K`

Putting values in above equation, we get:

`P* 10L=1.5* 0.0821\text{ L atm }mol^(-1)K^(-1)* 298K\\\\P=(1.5* 0.0821* 298)/(10)=3.67atm`

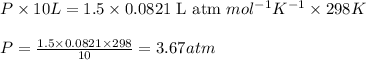
The partial pressure of a gas is given by Raoult's law, which is:

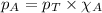`p_A=p_T* \chi_A` ......(1)

where,

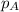`p_A` = partial pressure of substance A

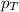`p_T` = total pressure

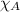`\chi_A` = mole fraction of substance A

To calculate the mole fraction of a substance, we use the equation:

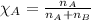`\chi_A=(n_(A))/(n_(A)+n_B)` .......(2)

We are given:

Moles of methane = 0.5 moles

Moles of hydrogen = 0.5 moles

Moles of sulfur dioxide = 0.5 moles

• For methane:

Using equation 2, we get:

`\chi_(CH_4)=(n_(CH_4))/(n_(CH_4)+n_(H_2)+n_(SO_2))=(0.5)/(1.5)=(1)/(3)`

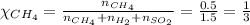
Using equation 1, we get:

`p_(CH_4)=3.67* (1)/(3)=1.22atm`

Partial pressure of methane = 1.22 atm

• For hydrogen gas:

Using equation 2, we get:

`\chi_(H_2)=(n_(H_2))/(n_(CH_4)+n_(H_2)+n_(SO_2))=(0.5)/(1.5)=(1)/(3)`

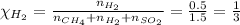
Using equation 1, we get:

`p_(H_2)=3.67* (1)/(3)=1.22atm`

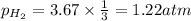
Partial pressure of hydrogen gas = 1.22 atm

• For sulfur dioxide:

Using equation 2, we get:

`\chi_(SO_2)=(n_(SO_2))/(n_(CH_4)+n_(H_2)+n_(SO_2))=(0.5)/(1.5)=(1)/(3)`

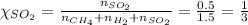
Using equation 1, we get:

`p_(SO_2)=3.67* (1)/(3)=1.22atm`

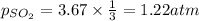
Partial pressure of sulfur dioxide = 1.22 atm

Hence, the partial pressure of individual components in the container will be same, that is
`p_(SO_2)=p_(CH_4)=p_(H_2)`