Question

How much energy is required to change a 120 g ice cube from ice at -11°C to steam at 165°C? Answer in J.

Answer 1

Answer: 357705.6 J

Explanation:

The conversions involved in this process are :

`(1):H_2O(s)(-11^0C)\rightarrow H_2O(s)(0^0C)\\\\(2):H_2O(s)(0^0C)\rightarrow H_2O(l)(0^0C)\\\\(3):H_2O(l)(0^0C)\rightarrow H_2O(g)(100^0C)\\\\(4):H_2O(l)(100^0C)\rightarrow H_2O(g)(100^0C)\\\\(5):H_2O(g)(100^0C)\rightarrow H_2O(g)(165^0C)`

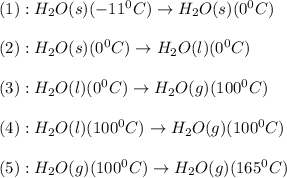
Now we have to calculate the enthalpy change.

`\Delta H=[m* c_(p,s)* (T_(final)-T_(initial))]+n* \Delta H_(fusion)+[m* c_(p,l)* (T_(final)-T_(initial))]+n* \Delta H_(vap)+[m* c_(p,g)* (T_(final)-T_(initial))]`

where,

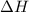`\Delta H` = enthalpy change = ?

m = mass of water = 120 g

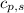`c_(p,s)` = specific heat of solid water = 2.09 J/gK

`c_(p,l)` = specific heat of liquid water = 4.18 J/gK

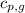`c_(p,g)` = specific heat of gaseous water = 1.84 J/gK

n = number of moles of water =
`\frac{\text{Mass of water}}{\text{Molar mass of water}}=(120g)/(18g/mole)=6.7mole`

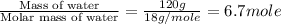
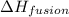`\Delta H_(fusion)` = enthalpy change for fusion = 6.01 KJ/mole = 6010 J/mole

`\Delta H_(vap)` = enthalpy change for vaporization = 40.67 KJ/mole = 40670 J/mole

Now put all the given values in the above expression, we get

`\Delta H=[120g* 4.18J/gK* (0-(-11))K]+6.7mole* 6010J/mole+[120g* 2.09J/gK* (100-0)K]+6.7mole* 40670J/mole+[120g* 1.84J/gK* (165-100)K]`

`\Delta H=357705.6J`

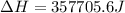
Therefore, the energy required to change a 120 g ice cube from ice at -11°C to steam at 165°C is, 357705.6 J