To solve this problem we will use the linear motion kinematic equations, for which the change of speed squared with the acceleration and the change of position. The acceleration in this case will be the same given by gravity, so our values would be given as,
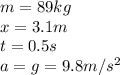
Through the aforementioned formula we will have to

The particulate part of the rest, so the final speed would be
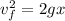
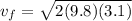

Now from Newton's second law we know that
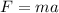
Here,
m = mass
a = acceleration, which can also be written as a function of velocity and time, then
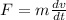
Replacing we have that,
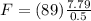
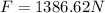
Therefore the force that the water exert on the man is 1386.62