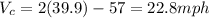Question

Use a system of equations to solve the following problem. A private jet flies the same distance in 7 hours that a commercial jet flies in 4 hours. If the speed of the commercial jet was 57 mph less than 2 times the speed of the private jet, find the speed of each jet.Speed of private jet =Speed of commercial jet =

Answer 1

`V_p = 39.9 mph`

`V_c = 2(39.9) -57=22.8 mph`

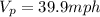
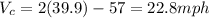
Explanation:

Notation and info given

Let's define some notation first:

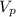`V_p` represent the speed for the Private's jet

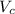`V_c` represent the speed for the Commercial jet

`x` represent the total distance traveled (variable of interest)

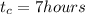`t_c = 7 hours` represent the time to travel a distance x for the commercial jet

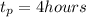`t_p = 4 hours` represent the time to travel a distance x for the private's jet

Solution to the problem

Since both jets are travelling the same distance we can set up the following equation:

`x_c = x_p`

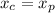
Form the definition of distance we know that
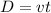`D = v t` and if we replace this we got this:

`V_c t_c = V_p t_p`

`V_c (7 hours) = V_p (4 hours)`

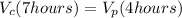
We know that also: "If the speed of the commercial jet was 57 mph less than 2 times the speed of the private jet", so then we have this expresion:

`V_c = 2 V_p -57`

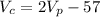
And if we replace this condition we got this:

`(2V_p -57) (7 hours) = V_p (4 hours)`

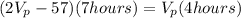
And we can find
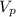`V_p` solving the equation like this:

`14 V_p - 399 = 4V_p`

`10 V_p = 399`

`V_p = 39.9 mph`

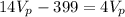
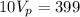
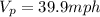
And now we can replace in order to find
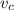`v_c` like this:

`V_c = 2(39.9) -57=22.8 mph`