Question

A parallel-plate capacitor has plates of area A. The plates are initially separated by a distance d, but this distance can be varied. The capacitor is connected to a battery.

a) What should the plate separation be if you want to halve the capacitance.

b)What should the plate separation be if you want to halve the capacitance.

c)What should the plate separation be if you want to halve the charge stored?

d) What should the plate separation be if you want to halve the charge stored?

e)What should the plate separation be if you want to halve the energy stored?

f)What should the plate separation be if you want to halve the energy stored?

g)What should the plate separation be if you want to halve the energy density?

Answer 1

a) In a parallel plate capacitor the capacitance is

`C = (Q)/(V) = \epsilon_0(A)/(d)`

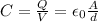
So, in order to halve the capacitance the plate separation should be twice the original distance.

b) Same question as (a).

c) According to the above equations, the charge stored in a capacitor is directly proportional to the plate separation.

`(Q)/(V) = (A)/(d)`

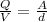
In order to halve the charge stored the plate separation should be half the original distance.

d) Same question as (c).

e) The energy stored in a capacitor is

`U = (1)/(2)CV^2 = (1)/(2)\epsilon_0(A)/(d)(Ed)^2 = (1)/(2)\epsilon_0AE^2d`

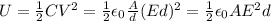
In order to halve the energy stored in the capacitor, the plate separation should be twice the original distance.

f) Same question as (e).

g) The energy density is given by the following equation

`u = ((1)/(2)CV^2)/(Ad) = ((1)/(2)\epsilon_0(A)/(d)(E^2d^2))/(Ad) = (1)/(2)\epsilon_0E^2.`

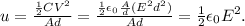
As it turns out, the energy density is independent from the geometric factors. This makes sense, because the electric field in a parallel field capacitor is independent from the distance.