The function g representing the area of the square as a function of the radius of the circle r is given as:
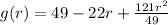
Solution:
Given that,
length of rope = 28 feet
Let "c" be the circumference of circle
Let "p" be the perimeter of square
Therefore,
length of rope = circumference of circle + perimeter of square
c + p = 28 ------- eqn 1
The circumference of circle is given as:
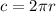
Where, "r" is the radius of circle
Substitute the above circumference in eqn 1
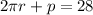
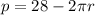 ----------- eqn 2
----------- eqn 2
If "a" is the length of each side of square, then the perimeter of sqaure is given as:
p = 4a
Substitute p = 4a in eqn 2
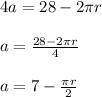
The area of square is given as:
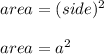
Substitute the value of "a" in above area expression
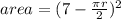 ------ eqn 3
------ eqn 3
We know that,
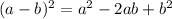
Therefore eqn 3 becomes,
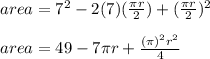
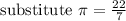
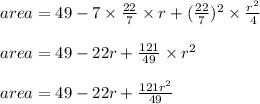
Let g(r) represent the area of the square as a function of the radius of the circle r, then we get
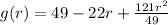
Thus the function is found