Question

Two pumps are used to empty a sewage tank. One pump pumps 60 gallons per minute (gpm) and the second pumps 50 gpm. They pumped for 30 minutes. How many total gallons are pumped?

Answer 1

330

Explanation:

Answer 2

The total gallons of sewage water pumped is 3300 gallons .

Explanation:

Given as :

Two pumps are used to empty a sewage tank.

The rate of pumping the tank by first pump = x = 60 gallons per minute

The rate of pumping the tank by second pump = y = 50 gallons per minute

Total time taken by both the pumps to empty tank = t = 30 minutes

Let The total gallons of sewage water pumped = z gallons

Now, According to question

Total rate of pumping the sewage tank with first and second pump = x + y

Or, Total rate of pumping the sewage tank with first and second pump = 60 gpm + 50 gpm

Or, Total rate of pumping the sewage tank with first and second pump = 110 gallons per min

Now, Total rate of pumping the sewage tank =
`(\textrm The total gallons of sewage water pumped)/(\textrm total time taken)`

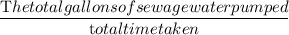
i.e total gallons of sewage water pumped = rate of pumping the sewage tank × total time taken

or, z = 110 gallons per min × t

Or, z = 110 gallons per min × 30 min

Or, z = 3300 gallons

So, The total gallons of sewage water pumped = z = 3300 gallons

Hence, The total gallons of sewage water pumped is 3300 gallons . Answer