Question

A lumber company is making doors that are 2058.0 millimeters tall. If the doors are too long they must be trimmed, and if the doors are too short they cannot be used. A sample of 17 is made, and it is found that they have a mean of 2047.0 millimeters with a standard deviation of 27.0. A level of significance of 0.1 will be used to determine if the doors are either too long or too short. Assume the population distribution is approximately normal. Is there sufficient evidence to support the claim that the doors are either too long or too short?

Answer 1

There is not enough evidence to support the claim that the doors are either too long or too short.

Explanation:

We are given the following in the question:

Population mean, μ = 2058.0 millimeters

Sample mean,
`\bar{x}` = 2047.0 millimeters

Sample size, n = 17

Alpha, α = 0.10

Sample standard deviation, s = 27

First, we design the null and the alternate hypothesis

`H_(0): \mu = 2058.0\text{ millimeter}\\H_A: \mu \\eq 2058.0\text{ millimeter}`

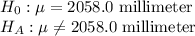
We use Two-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }`

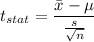
Putting all the values, we have

`t_(stat) = \displaystyle( 2047.0 - 2058.0)/((27)/(√(17)) ) = -1.6798`

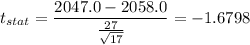
Now,
`t_(critical) \text{ at 0.10 level of significance, 16 degree of freedom } = \pm 1.7396`

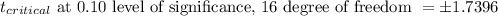
Since, the calculated t statistic lies in the acceptance region, we fail to reject the null hypothesis and accept the null hypothesis.

Thus, there is not enough evidence to support the claim that the doors are either too long or too short.