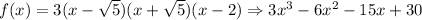Question

Which is the polynomial function of lowest degree with rational real coefficients, a leading coefficient of 3 and roots StartRoot 5 EndRoot and 2?

a) f (x) = 3 x cubed minus 6 x squared minus 15 x + 30
b) f (x) = x cubed minus 2 x squared minus 5 x + 10
c) f (x) = 3 x squared minus 21 x + 30
d) f (x) = x squared minus 7 x + 10

Answer 1

its a

Explanation:

Answer 2

`a) f(x)=3x^(3)-6x^(2)-15x+30`

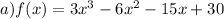
Explanation:

1) In this question we've been given "a", the leading coefficient. and two roots:

`x_(1)=√(5)\:x_(2)=2`

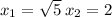
2) There's a theorem, called the Irrational Theorem Root that states:

If one root is in this form
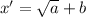`x'=√(a)+b` then its conjugate
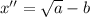`x''=√(a)-b`. is also a root of this polynomial.

Therefore

`x_3=-√(5)`

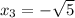
3) So, applying this Theorem we can rewrite the equation, by factoring. Remembering that x is the root. Since the question wants it in this expanded form then:

`f(x)=3(x-√(5))(x+√(5))(x-2)\Rightarrow 3x^(3)-6x^(2)-15x+30`