Question

Using the half-life of 5730 years, how many years would it take the 4.0 sample to decay to 0.25g

Answer 1

22920 years

Step-by-step explanation:

half- life : Time in which sample becomes half of its original value.

It is calculated by :

n = t /half-life

Age of the sample = n x (half - life)

here, n = number of half - life

4 ----> 2 ----> 1 ----> 0.5 ---->0.25 (divide the mass each time by 1/2 )

This is equal to 4 - half life

= 4 (5730)

=22920 years

SECOND METHOD

The following equation gives relation between the original Number of species at Zero time (No) and number of species after decays (N) in time t

`N = N_(0)e^(-\lambda t)`

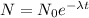
It is asked to calculate 't'.

`\lambda` = Decay constant

`\lambda = (0.693)/(t_(1/2))`

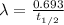
t1/2 = Half life = 5730 years

`\lambda = (0.693)/(5730)`

`\lambda= 1.209* 10^(-4)` per year

N= 0.25 g

No = 4.0 g

Insert the parameter in the formula and solve for t

`N = N_(0)e^(-\lambda t)`

`0.25 = 4e^-{1.209* 10^(-4)* t}`

`(0.25)/(4) = e^-{1.209* 10^(-4)* t}`

`0.0625 = e^-{1.209* 10^(-4)* t}`

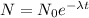
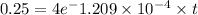
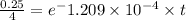
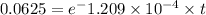
take ln(natural logarithm) both side,

`ln 0.0625 = ln(e^-{1.209* 10^(-4)* t})`

`-2.75=-1.209* 10^(-4)* t}`

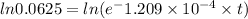
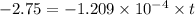
= 22932.9 years (approx to 22920)