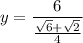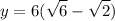Answer:
Step-by-step explanation:
Right Triangles
The right triangles are those who have an internal angle of 90°. There are certain relations that only stand in right triangles, where the larger side is called the hypotenuse and the other two are the legs. The trigonometric relations in a right triangle are:
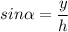
Where y is the opposite side to the angle
 and h is the hypotenuse. We also have
and h is the hypotenuse. We also have

In this formula, x is the adjacent side to
 . Finally, we have
. Finally, we have
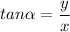
We cannot be sure what is the data and what are the results. We'll assume two given values: The base of the triangle x=6m and the angle adjacent to it
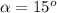
The sine, cosine, and tangent of some angles called notable or special angles are widely known. Some of these angles are 0°, 30°, 45°, 60°, 90°.
The triangle of this problem has an angle of 15° which trigonometric functions are not so notable, but with some research we find


With these values in mind, we can find the rest of the sides of the triangle. For example, to know the value of the hypotenuse, we set
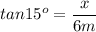
Solving for x

Similarily
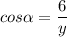
Solving for y