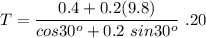Question

Please help me with the formular of this question and the solvings.​

Answer 1

`\displaystyle T=48.86\ N`

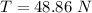
Step-by-step explanation:

Net Force

The second Newton's law explains how to understand the dynamics of a system where several forces are acting. The forces are vectorial magnitudes which means the x and y coordinates must be treated separately. For each component, the net force must equal the mass by the acceleration, i.e.

`F_(nx)=ma_x`

`F_(ny)=ma_y`

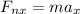
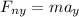
The box with mass m=20 kg is pulled by a rope with a
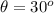`\theta= 30^o` angle above the horizontal. It means that force (called T) has two components:

`T_x=Tcos\theta`

`T_y=Tsin\theta`

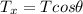
We'll assume the positive directions are to the right and upwards and that the box is being pulled to the right. There are two forces in the x-axis: The x-component of T (to the right) and the friction force (to the left). So the equilibrium equation for x is

`\displaystyle T\ cos\theta -Fr=m.a`

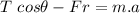
There are three forces acting in the y-axis: The component of T (upwards), the weight (downwards), and the Normal (upwards). Since there is no movement in the y-axis, the net force is zero and:

`\displaystyle N+T\ sin\theta -mg=0`

Rearranging:

`\displaystyle N+T\ sin\theta =mg`

Solving for N in the y-axis:

`\displaystyle N=mg-T\ sin\theta`

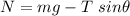
The friction force is given by

`\displaystyle Fr=\mu.N`

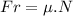
Replacing in the equation for the x-axis, we have

`\displaystyle T\ cos\theta -\mu\ N=ma`

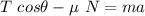
Replacing the formula for N in the equation for the x-axis

`\displaystyle T\ cos\theta -\mu(mg-T\ sin\theta)=ma`

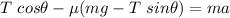
Operating and rearranging

`\displaystyle T\ cos\theta -\mu\ mg+T\ \mu\ sin\theta=ma`

`\displaystyle T\ (cos\theta +\mu\ sin\theta)=ma +\mu\ mg`

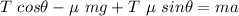
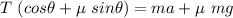
Solving for T:

`\displaystyle T=(a+\mu\ g)/(cos\theta +\mu\ sin\theta )\ m`

Plugging in the given values:

`\displaystyle T=(0.4+0.2(9.8))/(cos30^o+0.2\ sin30^o )\ .20`

`\boxed{\displaystyle T=48.86\ N}`