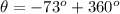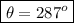Question

A ship is docked at an island that is 102.5 km south and 31.4 km east of the ship’s

port. What is the bearing of the island from the ship’s port of sail? Round your
answer to the nearest degree.

Answer 1

`\theta=287^o`

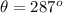
Explanation:

Position in the Plane

If we place an object in a plane and mesure its x and y coordinates, we are referencig its position according to the rectangular system. Other popular way to reference positions is in polar form or magnitude-angle form. If we have the rectangular coordinates (x,y), we can easily find the polar coordinates
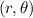`(r,\theta)` (and vice-versa). We use the formulas

`r=√(x^2+y^2)`

`\displaystyle tan\theta=(y)/(x)`

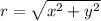
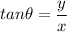
We have x=31.4 Km East (a positive coordinate) and y=-102.5 Km South (negative because it's pointing downwards). we need to find the angle respect to the East reference where
`\theta=0^o`. Check the image below for reference.

`\displaystyle tan\theta=(-102.5)/(31.4)=-3.264`

`\theta=-73^o`

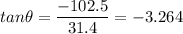
The angle can be also given as a positive quantity by adding 360^o

`\theta=-73^o+360^o`

`\boxed{\theta=287^o}`