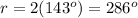Question

Angle r° = 2w°. What is the measure of angle r°?

A. 120 degrees
B. 286 degrees
C. 240 degrees
D. 143 degrees

Answer 1

b. 286!

Explanation:

Answer 2

Option B. 286 degrees

Explanation:

see the attached figure with letters to better understand the problem

step 1

Find the measure of angle BAD in triangle A

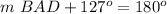`m\ BAD+127^o=180^o` ----> by supplementary angles (form a linear pair)

`m\ BAD=180^o-127^o=53^o`

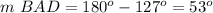
step 2

Find the measure of angle ABD in triangle A

we know that

The sum of the interior angles in any triangle must be equal to 180 degrees

so

`m\ BAD+m\ ADB+m\ ABD=180^o`

we have

`m\ BAD=53^o`

`m\ ADB=90^o`

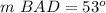
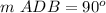
substitute

`53^o+90^o+m\ ABD=180^o`

`143^o+m\ ABD=180^o`

`m\ ABD=180^o-143^o`

`m\ ABD=37^o`

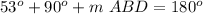
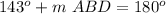
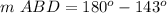
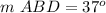
step 3

Find the measure of angle w

we know that

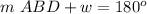`m\ ABD+w=180^o` ----> by supplementary angles (form a linear pair)

we have

`m\ ABD=37^o`

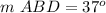
substitute

`37^o+w=180^o`

`w=180^o-37^o`

`w=143^o`

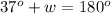
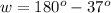
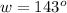
step 4

Find the measure of angle r

we have

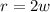`r=2w` ----> given problem

substitute the value of w

`r=2(143^o)=286^o`