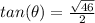Answer:
Part 1)
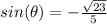
Part 2)
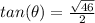
Explanation:
step 1
Find the
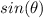
we know that
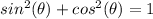
we have
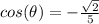
substitute
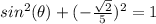
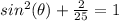
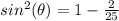
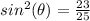
square root both sides
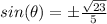
Remember that the angle θ terminates in Quadrant III
That means, that the value of sin(θ) is negative
so
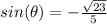
step 2
Find the
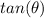
we know that
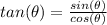
we have
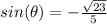
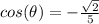
substitute
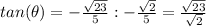
simplify