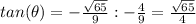Answer:
Part 1)

Part 2)
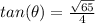
Explanation:
we have that
The cosine of angle theta is negative and the tangent of angle theta is positive
That means that the sine of angle theta is negative
step 1
Find
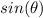
we know that
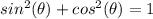
we have
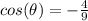
substitute
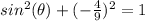
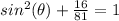
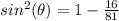

square root both sides
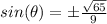
Remember that
In this problem the sine of angle theta is negative
so

step 2
Find
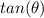
we know that
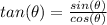
we have

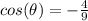
substitute the given values