Question

Triangle A has side lengths of 10 units, 24, units, and 26 units. Ryan cut out 2 copies of triangle A and joined them together to form a rectangle. What is the perimeter of the rectangle formed when the two triangles are joined?

Answer 1

Perimeter of Rectangle will be 68 units.

Explanation:

Given:

Length of side 1 = 10 units

Length of side 2 = 24 units

Length of side 3 = 26 units

Now we will check whether the triangle A is right angle triangle or not;

`(Length of side 3)^(2) = 26^2 = 676`

`(Length of side 2)^(2) = 24^2 = 576`

`(Length of side 1)^(2) = 10^2 = 100`

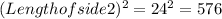
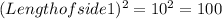
Now From above we can see that;

676 = 576 + 100

Hence we can say ;

`(Length of side 3)^(2) = ](Length of side 2)^(2) + (Length of side 1)^(2)`

By Converse of Pythagoras theorem.

"Hence When the square of the length of the hypotenuse is equal to sum of the square of other two sides we can say that triangle is a right angled triangle."

Now Given:

Ryan cut out 2 copies of triangle A and joined them together to form a rectangle.

So we can say that the hypotenuse side of the triangle will become diagonal of the rectangle and other two side will become length and width.

Now;

Length of rectangle = 24 units

Width of rectangle = 10 units.

We need to find the perimeter of rectangle.

Now Perimeter of rectangle is 2 times sum of Length and width.

framing in equation form we get;

Perimeter of rectangle =
`2(l+w) = 2* (24+10) = 2* 34 =68 units.`

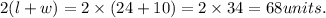
Hence Perimeter of Rectangle will 68 units.