Answer: OPTION B.
Explanation:
Below are some transformations for a function f(x):
1. If
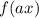 and
and
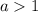 , the function is compressed horizontally by a factor of
, the function is compressed horizontally by a factor of
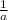 .
.
2. If
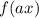 and
and
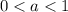 , the function is stretched horizontally by a factor of
, the function is stretched horizontally by a factor of
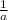 .
.
3. If
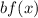 and
and
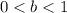 , the function is compressed vertically by a factor of "b".
, the function is compressed vertically by a factor of "b".
4. If
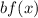 and
and
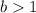 , the function is stretched vertically by a factor of "b".
, the function is stretched vertically by a factor of "b".
In this case you have the function f(x):
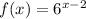
And the function g(x):
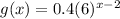
So, you can identify that:
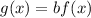 and
and
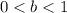
Therefore, the graph of the function g(x) is a vertical compression of the graph of function f(x).