Please help! :) A sector of a circle has a central angle measuring 15 degrees and the radius of the circle measures 9 inches. What is the arc length of the sector? Express the a…

Question

asked Nov 22, 2021 211k views

2 Answers

Eugene Kuleshov · Answer 1 · 2021-11-26T06:41:19+0000

Answer:

Second option is correct

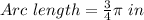
$Arc\ length = (3)/(4) \pi\ in$

Explanation:

Given:

Central angle = 15°

Radius of the circle = 9 in

Arc length = ?

Given formula is

$(Arc\ length)/(Circumfrance) = (n)/(360)$

Where n is the central angle of the sector.

Write the given formula for Arc length of the sector.

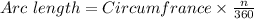
$Arc\ length = Circumfrance* (n)/(360)$

We know that the the circumference of the circle is
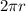$2\pi r$ , where r is the radius of the circle,

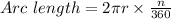
$Arc\ length = 2\pi r* (n)/(360)$

Now we substitute central angle value and radius value in above equation.

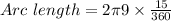
$Arc\ length = 2\pi 9* (15)/(360)$

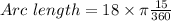
$Arc\ length = 18* \pi (15)/(360)$

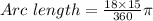$Arc\ length = (18* 15)/(360) \pi$ ----------(
(18)/(360)=(1)/(20) )

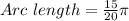
$Arc\ length = (15)/(20) \pi$

Divide the numerator and denominator by 5.

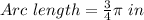
$Arc\ length = (3)/(4) \pi\ in$

Therefore the arc length of the sector is
$(3)/(4) \pi\ in$