Question

The axis of symmetry for the graph of the function f(x)=3x2+bx+4 is x equals three-halves. What is the value of b?

Answer 1

b = -9.

Explanation:

f(x)=3x2+bx+4 Convert to vertex form:

= 3(x^2 + (b/3)x) + 4

= 3 [ ( x + b/6)^2 - (b/6)^2] + 4

So the axis of symmetry is x = -b/6 = 3/2

so -2b = 18

b = -9.

Answer 2

The value of b is -9.

Explanation:

The given function is

`f(x)=3x^(2) +bx+4`

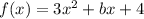
We know by given, the axis of symmetry is
`x=(3)/(2)`

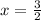
According to the theory, the axis of symmetry of a parabola is a vertical line that intercepts its vertex at its horizontal coordinate, which can be found we this formula

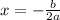`x=-(b)/(2a)` Where
`a=3`

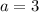
Know we just need to replace all given values and solve for
`b`

`x=-(b)/(2a)}\\(3)/(2) =-(b)/(2(3))\\(3)/(2)=-(b)/(6)\\ b=-(6(3))/(2) \\b=-9`

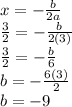
Therefore, the value of b is -9.